FAQ > Vibration G-force by Jay Tang, Eng.

G-force of Vibration Plate

G-force is a key indicator of vibration intensity. It provides a consistent basis for comparing the performance of vibration plates operating at different frequencies and amplitudes.

Although commonly called "G-force", it is not actually a force; rather, it is acceleration expressed in units of gravitational acceleration (G).

Why using G-force to express acceleration?

When studying how acceleration affects the human body, G-force is commonly used because it expresses acceleration relative to gravity, a well-understood reference we live with on Earth.

Compared to the standard acceleration unit m/s², G‑force makes it easier for us to comprehend how acceleration influences our body and to guage its magnitude.

1G = 9.81m/s at sea level²

When resting on the ground, we constantly experience 1G. By contrast, a fighter-jet pilot may experience up to 9G during a steep pull-up maneuver.

Since vibration plates are designed for physical exercise, expressing acceleration in G‑force helps users better grasp and evaluate vibration intensity.

This article provides a practical method to calculate the G‑force of a vibration plate.

Vibration Acceleration

Acceleration (a) is defined as the rate at which velocity changes over time, or how quickly the speed changes over a given period of time:

a = Δv/Δt

Unlike one-directional motion, vibration motion periodically reverses direction, producing acceleration patterns that differ from one-directional movement.

Characteristics of Vibration Acceleration

Fluctuating Acceleration Vibration acceleration (vibration G‑force) fluctuates continuously throughout a vibration cycle.

4 Distinct Phases According to its motion pattern, a vibration cycle can be divided into 4 distinct phases, each with its unique acceleration profile.

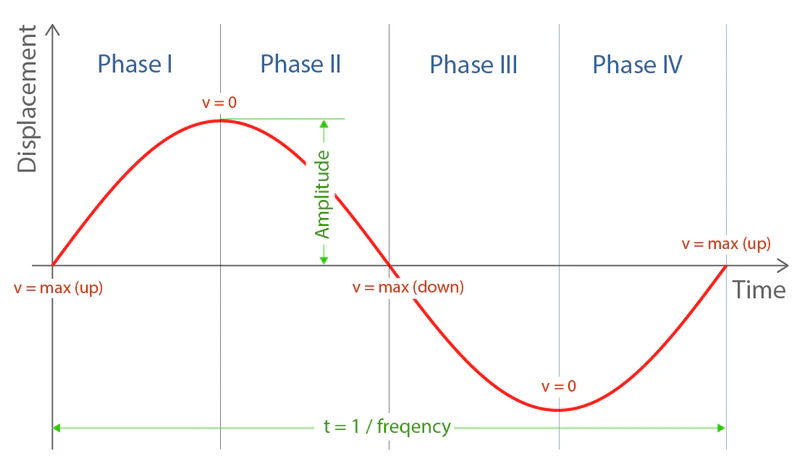
The sine diagram below presents the motion pattern of a vibration cycle.

4 Phases of a Vibration Cycle

Phase I	Phase II	Phase III	Phase IV
Moving upward	Moving downward	Moving downward	Moving upward
Velocity max→0	Velocity 0→max	Velocity max→0	Velocity 0→max
Deceleration	Acceleration	Deceleration	Acceleration

Phase IV When exercising on a vibration plate, Phase IV is the only phase that produces a positive upward acceleration, adding to the effect of gravity and creating additional downward load for effective muscle work.

Simple Harmonic Model

In physics study, Simple Harmonic Model (SHM) is commonly used to analyze vibration motion.

Displacement and time are represented and replaced by amplitude and frequency to calculate velocity and acceleration in SHM.

SHM Velocity and Acceleration Formula:

v = (2πf)Acon(2πft)

a = (2πf)²Asin(2πft)

where:

a = acceleration (m/s²)
v = velocity (m/s)
π = 3.14

f = frequency (Hz)
A = amplitude (meters)
t = time (seconds)

These two formulas calculate the instantaneous velocity and acceleration at a given point on the time line. The sine/cosine factor varies in the range between -1 and 1, resulting in:

v_max = ±(2πf)A

a_max = ±(2πf)²A

Vibration acceleration fluctuates between a positive maximum and negative maximum.

Then, what is the value to be asigned to represent the fluctuating vibration acceleration (G-force) for vibration plate?

Instead of using the instataneous fluctuating acceleration, we examine the motion pattern phase by phase and introduce a phase-based interval acceleration.

Phase-Interval Acceleration

A vibration cycle can be divided into 4 phases with distinct velocity and acceleration profiles.

Phase-Interval Acceleration (a_phase) is the acceleration over the entire phase period.

Compared to the fluctuating instantantaneous acceleration, Phase-Interval Acceleration practically represents the acceleration of each respective phase.

Calculation of Phase-Interval Acceleration based on the basic acceleration formula:

a_phase = Δv/Δt

where:

Δv = v_max - 0 = ±(2πf)A - 0
Δt = 1/(4f) (duration of a single phase)

therefore:

Phase-Interval Acceleration Calculation
Phase	I	II	III	IV
Δv	-(2πf)A	(2πf)A	-(2πf)A	(2πf)A
Δt	1/(4f)	1/(4f)	1/(4f)	1/(4f)
a_phase	-8πf²A	8πf²A	-8πf²A	8πf²A

Converting to Phase-Interval G-force (1G = 9.81 m/s²), and substituting the π ( π≈3.14):

Phase-Interval G-force Calculation
Phase	I	II	III	IV
Phase‑Interval G‑force	-2.56f²A Upward	2.56f²A Downward	-2.56f²A Downward	2.56f²A Upward

Vibration Plate Nominal G‑force

Phase IV G-force

For a vibration plate, Phase IV is the only phase in a vibration cycle that produces positive upright G‑force, which produces extra downward load on the user's body, adding to the effect of gravity and enhancing the muscle work during vibration exercise.

Therefore, Phase IV G-force properly represents the effective intensity of a vibration plate, and practically serves as the nominal vibration G‑force to reference, compare and assess vibration intensity for studying the influence on the human body from the vibration plate.

Nominal G-force of Vibration Plate

We define the upward, positive Phase IV G-force of a vibration plate as its Nominal G‑force.

Nominal G-force (Phase IV G-force) of Vibration Plate:

Nominal G-force = 2.56f²A

where:

f = frequency (Hz)

A = amplitude (meters)

Using the phase-interval based Nominal G-force to represent the fluctuating vibration G-force is more accurate and practical than using the instantaneous maximum G‑force.

Why Nominal G-force?

For comparison, the instantaneous maximum vibration G-force is calculated as:

G-force _max = (2πf)²/9.81 = 4.02f²A

Phase IV G‑force Calculation Examples

Model#	VT007	VT009	VT003F	VT027
Type	Linear Vibration	Linear Vibration	Linear Vibration	Pivotal Oscillation
Frequency	40Hz	40Hz	40Hz	14Hz
Amplitude Peak‑to‑Peak*	1.6mm	1.8mm	1.5mm	10mm
Amplitude	0.8mm	0.9mm	0.75mm	5mm
Nominal G‑Force	3.3	3.7	3.1	2.5
Max G‑Force	5.1	5.8	4.8	3.9

* The amplitude quoted for a vibration plate typically refers to the peak-to-peak displacement—which is twice the one-way (single-sided) amplitude used in the formula.

Note: Body Weight and G-force

Body weight is not a variable in G-force's calculation. However, for linear vibration plate, the amplitude yield to the user's body weight. So different body weight causes different G‑force.

For pivotal oscillation type of vibration plate, body weight does not affect G‑force.

Summary and Verification

G-force is acceleration, not force. G-force is acceleration expressed relative to gravitational acceleration (G), which makes the magnitude easier to understand than using the unit m/s².
Vibration acceleration fluctuates. During each vibration cycle, acceleration continually changes between positive and negative maximum values, so a single instantaneous peak value does not adequately represent the vibration intensity a user experiences.
Phase-interval acceleration provides a practical metric. By dividing the vibration cycle into four phases and calculating the interval acceleration in each phase, we obtain a realistic representation of how acceleration behaves over time..
Phase IV G-force captures the exercise-relevant load. Phase IV is the only phase that produces a positive upright G-force that adds to gravity and increases the downward load on the user’s body, which is what contributes most to muscle loading during vibration exercise.
The Phase IV G-force formula is scientifically consistent. By applying the basic acceleration definition (a = Δv / Δt) to Phase IV and converting to G-force, we obtain the Phase IV G-force as the nominal vibration G-force:
Nominal G-force = 2.56 f²A
where f is frequency in Hz and A is amplitude in meters.
This formula provides a practical and comparable way to quantify and assess the intensity of a vibration plate.

Although numerous studies evaluate vibration frequency, displacement, and peak acceleration, no standardized method exists for defining a representative G-force for vibration plates. This article introduces a phase-based mechanical model and the nominal G-force to fill this gap.