VT007 Amplitude & G-force

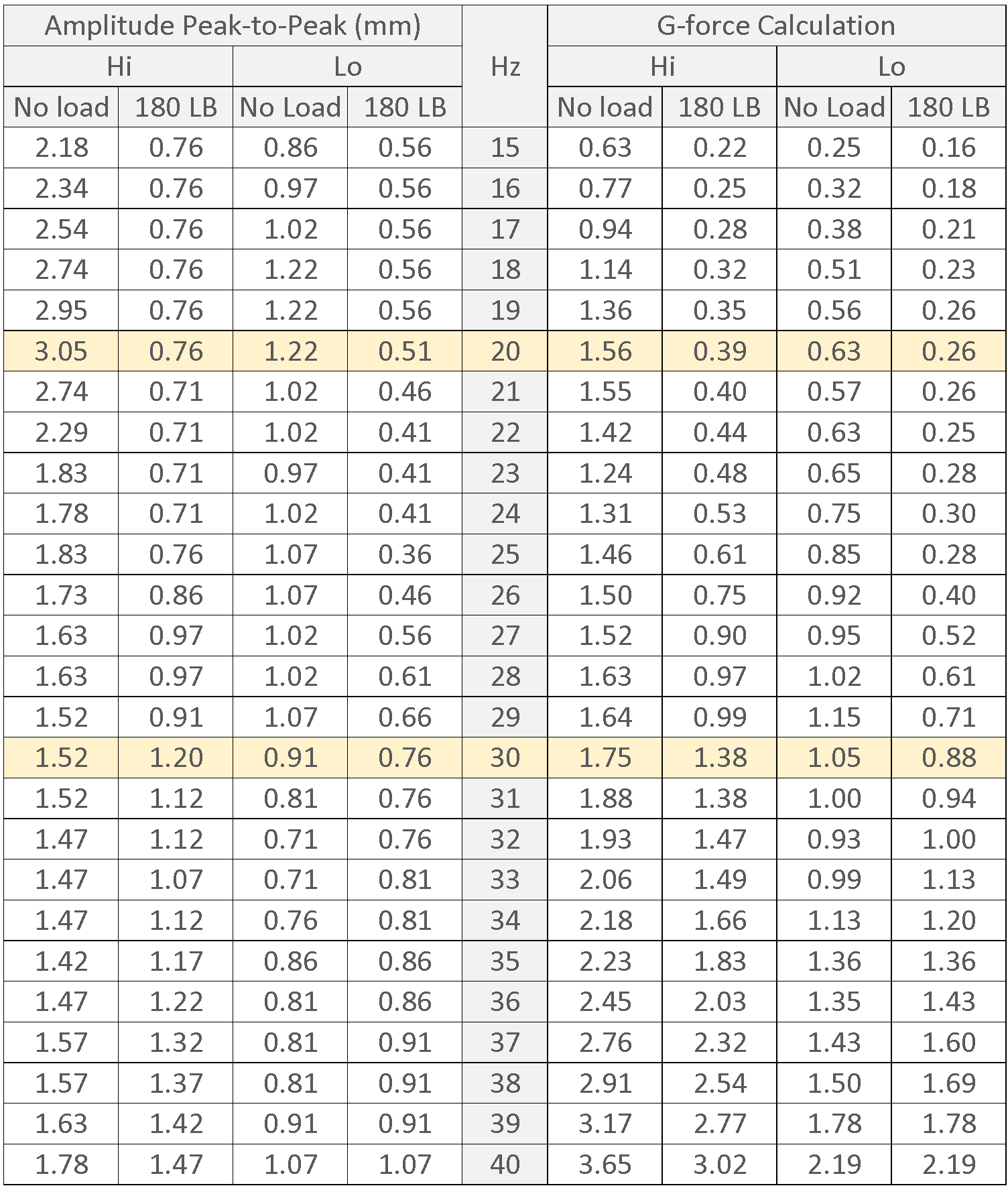
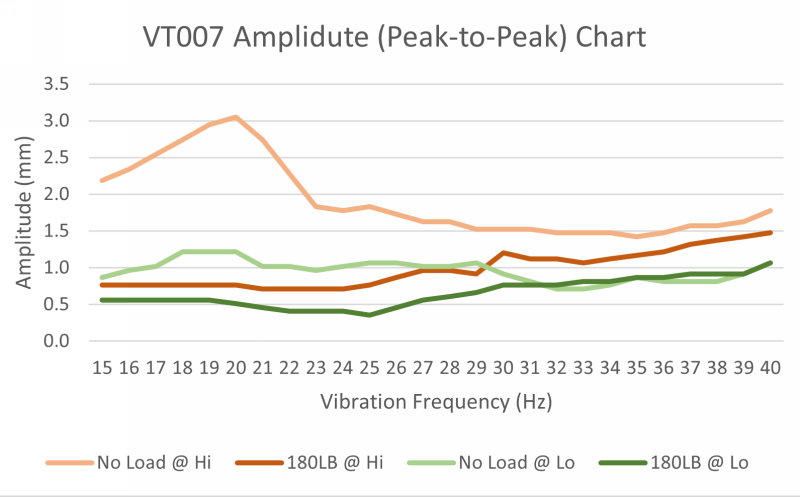
Two randomly selected VT007 vibration plates are tested to measure using a dial indicator for their average vertical peak‑to‑peak amplitude with the following variables:
- Amplitude settings: Hi and Lo
- Vibration Frequency: 15Hz - 40Hz
- Load (body weight): No load and 180 lb
Nonimal G-froce values are calculated based on the average measured amplitude value.
Peak-to-Peak Amplitude & Nominal G-force